Protecting the pay zone from damage is critical to realize the full potential of any well. Reservoir drill-in fluids (RDF) are designed to prevent formation damage due to fluid invasion and solids plugging. A poorly designed RDF may react with the formation fluid creating blockage or restriction for the natural flow of the reservoir. A large range of undesired solid particles from drill solids, fluid chemicals and clay viscosifiers may end up plugging the reservoir pores. The technique for designing a non-damaging RDF is to start with selecting bridging agents with an ideal size distribution to effectively seal the formation surface.

We are going to list a couple of theories behind bridging agent size selection.

1. Abrams’ rule
   Abrams [1] proposed a rule for formulating minimally invading, non-damaging drill-in fluids. This rule states that the mean particle size of the bridging agent should be equal to or slightly greater than 1/3 the medium pore size of the targeted formation. For example, the rule predicted that those 50μm bridging particles should be effective at sealing pores up to or around 150μm in diameter. Abrams also suggested that the concentration of the bridging solids used should be at least 5% by volume (50 lb/bbl or 150 kg/m3) of the solids in the fluid.
   However, Abrams only addresses the particle size that initiates a bridge. His rule does not give the optimum size or address the best packing sequence of a particle size for minimizing fluid invasion and optimizing sealing. The fluid design using these guidelines tends to use a wide range of particles in an attempt to provide a wide range of bridging capabilities.
2. Ideal Packing Theory (IPT)
   Ideal Packing Theory can be defined as a full range of particle size distribution required to effectively seal all voids, including those created by bridging agents.
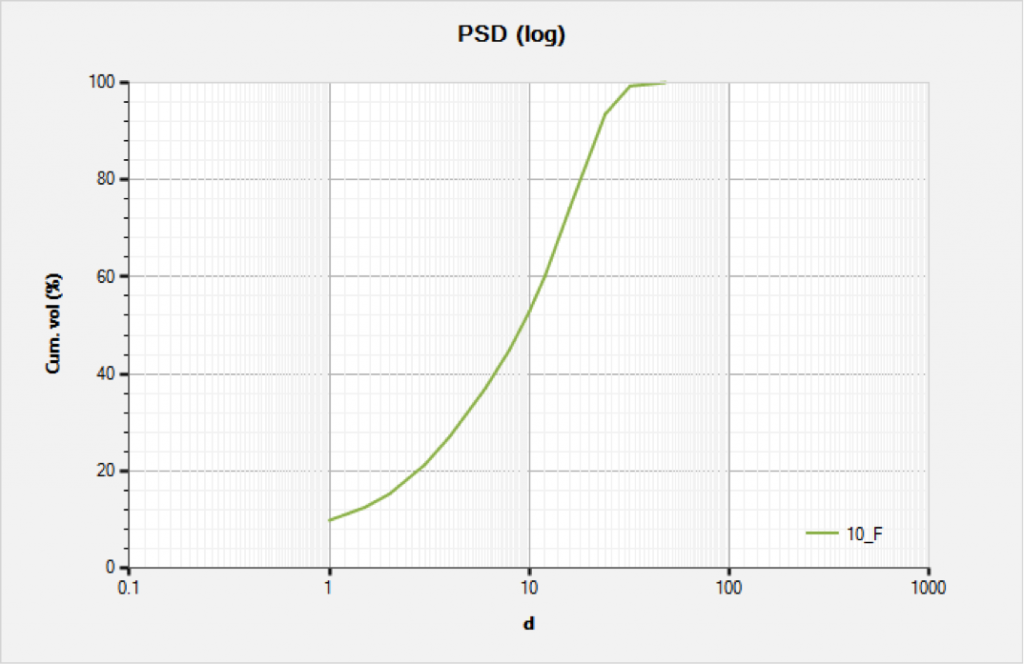
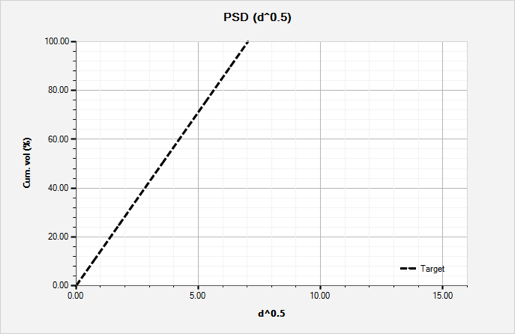
   Fig. 1 shows a typical particle-size distribution for a solid bridging material. Generally, the cumulative volume curve forms an S-shape when plotted on semi-log coordinates. Any commercially available particle-size analysis devices can generate these S-shape plots.
   

   Fig 1. PSD of a Commercial Bridging Product

   Kaeuffer [2] employed theories for particles by Furnas and Fuller-Bollomey to generate a simple Ideal Packing Theory also known as the D^½ rule. This rule states that ideal packing occurs when the percent of cumulative volume vs. the D^½ forms a straight-line relationship as shown in Fig. 2, where D^½ is square root of the particle diameter. These subsequent layering of bridging agents results in a tighter and less invading filter cake.

   

   Fig 2. Ideal Packing

References:

1. Abrams, A.: “Mud Design to Minimize Rock Impairment Due to Particle Invasion,” JPT (May 1977) 586.
2. Kaeuffer M.: Determination de L'Optimum deRemplissage Granulometrique et Quelques proprieties S’y Rattachant. Presented at Congres International de I’A.F.T.P.v., Rouen, Oct. 1973